图 (Graph):图是一个二元组 $(V, E)$,其中 $V, E$ 为集合 (多重集),图常用 $G, H$ 等表示,如:$G = (V, E)$。
图分为无向图 (Undirected graph) 和有向图 (Directed graph) 两种,若 $G$ 为无向图,则 $E$ 中的每个元素为一个无序二元组 $(u, v)$,称作无向边 (Undirected edge),简称边 (Edge),其中 $u, v \in V$。设 $e = (u, v)$,则 $u, v$ 称为 $e$ 的端点 (End-vertex)。
若 $G$ 为有向图,则 $E$ 中的每一个元素为一个 (有序) 二元组 $(u, v)$,有时也写作 $u \to v$,称作有向边 (Directed edge) 或弧 (Arc),在不引起混淆的情况下也可以称作边。设 $e = u \to v$,则此时 $u$ 称为 $e$ 的起点 (Origin),$v$ 称为 $e$ 的终点 (Terminus),起点和终点也称为 $e$ 的端点。
对于 $V$ 中的每个元素,我们称其为顶点 (Vertex)或节点 (Node),简称点 (Vertex),顶点的集合称为点集 (Vertex set),边的集合称为边集 (Edge set)。
图 $G$ 的点集和边集可以表示为 $V(G)$ 和 $E(G)$,在不引起混淆的情况下,也能表示成 $V, E$。图 $G$ 的点数 $\left| V(G) \right|$ 也被称作图 $G$ 的阶 (Order)。
简单图 (Simple graph):若一个图中没有自环和重边时,它被称为简单图。
自环 (Loop):对 $E$ 中的边 $e = (u, v)$,若 $u = v$,则 $e$ 被称作一个自环。
重边 (Multiple edge):若 $E$ 中存在两个完全相同的元素 (边) $e_1, e_2$,则它们被称作 (一组) 重边。
如果一张图中有自环或重边,则称它为重图 (Multigraph)。
Warning 1:在无向图中 $(u, v)$ 和 $(v, u)$ 算一组重边,而在有向图中,$u \to v$ 和 $v \to u$ 不为重边。
Warning 2:在题目中,如果没有特殊说明,默认存在自环和重边,在做题时需特殊考虑。
在无向图 $G = (V, E)$ 中,若点 $v$ 是边 $e$ 的一个端点,则称 $v, e$ 是关联的 (Incident) 或相邻的 (Adjacent)。对于两个顶点 $u, v$,若存在一条边与它们均关联,则称 $u, v$ 是相邻的 (Adjacent)。
一个顶点 $v \in V$ 的邻域 (Neighborhood) 是这样一个集合:它是所有与之相邻的顶点所构成的集合,记作 $N(v)$。
一个点集 $S$ 的邻域是这样一个集合:它是所有与 $S$ 中至少一个点相邻的集合,记作 $N(S)$。由定义,$$ N(S) = \bigcup_{v \in S} N(v) $$
与一个顶点 $v$ 关联的边的条数称作该顶点的度 (Degree) (或次数),记作 $d(v)$。特别地,对于边 $(v, v)$,则每条这样的边要对 $d(v)$ 产生 $2$ 的贡献。
对于无向简单图,有 $d(v) = \left| N(v) \right|$。
对于任何无向图 $G = (V, E)$,有 $$ \sum_{v \in V} d(v) = 2 \left| E \right| \tag 1 \label 1 $$
- 若 $d(v) = 0$,则称 $v$ 为孤立点 (Isolated vertex)。
- 若 $d(v) = 1$,则称 $v$ 为叶节点 (Leaf vertex)/悬挂点 (Pendant vertex)。
- 若 $2 \mid d(v)$,则称 $v$ 为偶点 (Even vertex)。
- 若 $2 \nmid d(v)$,则称 $v$ 为奇点 (Odd vertex)。由 $\eqref 1$,图中奇点的个数是偶数。
- 若 $d(v) = \left| V \right| - 1$,则称 $v$ 为支配点 (Universal vertex) (不常见)。
对一张图,所有顶点的度数的最小值称为 $G$ 的最小度 (Minimum degree),记作 $\delta (G)$;最大值称为最大度 (Maximum degree),记作 $\Delta (G)$。
则有 $\displaystyle \delta (G) = \min_{v \in G} d(v); \Delta (G) = \max_{v \in G} d(v)$。
在有向图 $G = (V, E)$ 中,以一个顶点 $v$ 为起点的边的条数称为该顶点的出度 (Outdegree),记作 $d^+(v)$。以一个顶点 $v$ 为终点的边的条数称为该顶点的入度 (Indegree),记作 $d^-(v)$。
对于任何有向图 $G = (V, E)$,有 $$ \sum_{v \in V} d^+(v) = \sum_{v \in V} d^-(v) = \left| E \right| \tag 2 \label 2 $$
若对一张无向图 $G = (V, E)$,每个顶点的度数都是一个固定的常数 $k$,则称 $G$ 为 $k-$正则图 ($k-$Regular Graph)。
对两个阶数相等的简单图 $G, H$,如果存在一个双射 $f : V(G) \to V(H)$,满足对于两个顶点 $u, v$ ($u \neq v$),$u, v$ 在 $G$ 中相邻当且仅当 $f(u)$ 和 $f(V)$ 在 $H$ 中相邻,则我们称 $f$ 为 $G$ 到 $H$ 的一个同构 (Isomorphism),且图 $G$ 与图 $H$ 是同构的 (Isomorphic),记作 $G \cong H$。
途径 (Walk):一个点和边的交错序列,其中首尾是点——$v_0, e_1, v_1, e_2, v_2, \cdots, e_k, v_k$,有时简写为 $v_0 \to v_1 \to v_2 \to \cdots \to v_k$。其中 $e_i$ 的两个端点分别为 $v_{i-1}$ 和 $v_i$ (以下默认设 $w = \left[ v_0, e_1, v_1, e_2, v_2, \cdots, e_k, v_k \right]$)。
迹 (Trail):对于一条途径 $w$,若 $e_1, e_2, \cdots, e_k$ 两两互不相同,则称 $w$ 是一条迹。
路径 (Path) (又称简单路径 (Simple path)):对于一条迹 $w$,除了 $v_0$ 和 $v_k$ 允许相同外,其余点两两互不相同,则称 $w$ 是一条路径。
回路 (Circuit):对于一个迹 $w$,若 $v_0 = v_k$,则称 $w$ 是一个回路。
环/圈 (Cycle) (又称简单回路 (Simple circuit)):对于一条简单路径 $w$,若 $v_0 = v_k$,则称 $w$ 是一个环。
对于一张无向图 $G = (V, E)$,对于 $u, v \in V$,存在一条途径使得 $v_0 = u, v_k = v$,则称 $u, v$ 是连通的 (Connected)。由定义,任意一个顶点和自身连通,任意一条边的两个端点连通。
若无向图 $G = (V, E)$,满足其中任意两个顶点均连通,则称 $G$ 是连通图 (Connected graph),$G$ 的这一性质称作连通性 (Connectivity)。
对一张图 $G = (V, E)$,若存在另一张图 $H = (V', E')$ 满足 $V' \subseteq V; E' \subseteq E$,则称 $H$ 是 $G$ 的子图 (Subgraph),记作 $H \subseteq G$。
若对 $H \subseteq G$,满足对 $\forall u, v \in V'$,只要 $(u, v) \in E$,均有 $(u, v) \in E'$,则称 $H$ 是 $G$ 的导出子图/诱导子图 (Induced subgraph)。
容易发现,一个图的导出子图仅由子图的点集决定,因此点集为 $V'$ ($V' \subseteq V$) 的导出子图称为 $V'$ 导出的子图,记作 $G \left[ V' \right]$。
若 $H \subseteq G$ 满足 $V' = V$,则称 $H$ 为 $G$ 的生成子图/支撑子图 (Spanning subgraph)。
如果一张无向图 $G$ 的某个生成子图 $F$ 为 $k-$正则图,则称 $F$ 为 $G$ 的一个 $k-$因子 ($k-$Factor)。
如果有向图 $G = (u, v)$ 的导出子图 $H = G \left[ V^* \right]$ 满足 $\forall v \in V^*, (v, u) \in E$,就有 $u \in V^*$,则称 $H$ 为 $G$ 的一个闭合子图 (Closed subgraph)。
对于无向简单图 $G = (V, E)$,它的补图 (Complement graph)指的是这样的一张图,记作 $\bar G$,满足 $V \left( \bar G \right) = V \left( G \right)$,且对任意顶点对 $(u, v)$,$(u, v) \in E \left( G \right)$ 当且仅当 $(u, v) \notin E \left( G' \right)$。
一些特殊的无向简单图:
若 $G = \left( V, E \right)$ 满足,$\forall u, v \in V, u \neq v$,均有 $(u, v) \in E$,则称 $G$ 为完全图 (Complete graph),$n$ 阶完全图记作 $K_n$。
若 $G = \left( V, E \right)$ 满足 $E = \varnothing$,则称 $G$ 为零图 (Null graph),$n$ 阶零图记作 $N_n$。易知,$N_n$ 为 $K_n$ 互为补图。
若 $G = \left( V, E \right)$ 的所有边恰好构成一个圈,则称 $G$ 为环/圈图 (Cycle graph),$n$ ($n \geq 3$) 阶圈图记作 $C_n$。易知,一张图为圈图的充分必要条件是,它是 $2-$正则连通图。
若 $G = \left( V, E \right)$ 满足,存在一个点 $v$ 为支配点,其余点之间没有边相连,则称 $G$ 为星图/菊花图 (Star graph),$n + 1$ ($n \geq 1$) 阶星图记作 $S_n$。
若 $G = \left( V, E \right)$ 满足,存在一个点 $v$ 为支配点,其它点之间构成一个圈,则称 $G$ 为轮图 (Wheel Graph),$n + 1$ ($n \geq 3$) 阶轮图记作 $W_n$。
若 $G = \left( V, E \right)$ 的所有边恰好构成一条简单路径,则称 $G$ 为链 (Chain/Path Graph),$n$ 阶的链记作 $P_n$。易知,一条链由一个圈图删去一条边而得。
立方体图 (Hypercube graph) 的定义见 #13。
如果一个无向连通简单图没有圈,则称它是一棵树 (Tree)。
非空的 $n$ 阶树恰好有 $n - 1$ 条边。这既是无圈图的边数上限,也是连通图的边数下限。
链和星图都是特殊的树。
如果一个图由若干棵不相交的树构成,则称它是一个森林 (Forest)。易知,一个无向简单图是森林的充要条件是,它没有圈。
由 $\eqref 1$,树至少有两个叶节点。
对于无向简单图,我们可以定义如下二元运算:
交 (Intersection):两张图 $G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)$ 的交定义成图 $G \cap H = \left( V_1 \cap V_2, E_1 \cap E_2 \right)$。
容易证明两个无向简单图的交还是无向简单图。
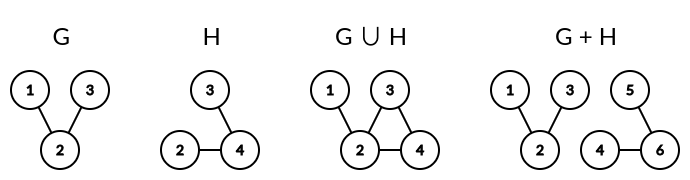
并 (Union):两张图 $G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)$ 的并定义成图 $G \cup H = \left( V_1 \cup V_2, E_1 \cup E_2 \right)$。
和 (Sum)/直和 (Direct sum) (注意与并的区别):对于 $G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)$,任意构造 $H' \cong H$ 使得 $V \left( H' \right) \cap V_1 = \varnothing$ ($H'$ 可以等于 $H$)。此时与 $G \cup H'$ 同构的任何图称为 $G$ 和 $H$ 的和/直和/不交并,记作 $G + H$ 或 $G \oplus H$。
若 $G$ 与 $H$ 的点集本身不相交,则 $G \cup H = G + H$。
比如,森林可以定义成若干棵树的和。
例子:设 $G = \left( \{1, 2, 3\}, \{(1, 2), (2, 3)\} \right), H = \left( \{2, 3, 4\}, \{(2, 4), (3, 4)\} \right)$,则 $G \cup H = \left( \{1, 2, 3, 4\}, \{(1, 2), (2, 3), (2, 4), (3, 4)\} \right)$,而 $G + H$ 可以表示为 $\left( \{1, 2, 3, 4, 5, 6\}, \{(1, 2), (2, 3), (4, 6), (5, 6)\} \right)$。
笛卡尔积 (Cartesian product):对 $G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)$,令 $V = V_1 \times V_2$ 为两个点集的 Cartesian 积,取 $\forall (u_1, u_2), (v_1, v_2) \in V$,其中 $u_1, v_1 \in V_1; u_2, v_2 \in V_2$。
令 $E$ 满足,$\left( \left( u_1, u_2 \right), \left( v_1, v_2 \right) \right) \in E$ 当且仅当 $\left( u_1 = v_1 \wedge \left( u_2, v_2 \right) \in E_2 \right) \vee \left( \left( u_1, v_1 \right) \in E_1 \wedge u_2 = v_2 \right)$。则 $G$ 和 $H$ 的 Cartesian 积定义为 $G \boxdot H = \left( V, E \right)$。
例子:下图中,左边和上面两张图的 Cartesian 积是右边那张图。

#11 拓展:定义立方体图 (Hypercube graph) $Q_n$ 满足:
$Q_0 = K_1, Q_1 = K_2, Q_n = Q_{n-1} \boxdot Q_1 (n \geq 2)$。
易知 $Q_2 \cong C_4$,$Q_3$ 为平面立方体的展开图。
$Q_n$ 是 $2^n$ 阶图,有 $2^{n-1} n$ 条边,是 $n-$正则图。
张量积 (Tensor product):对 $G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)$,令 $V = V_1 \times V_2$ 为两个点集的 Cartesian 积,取 $\forall (u_1, u_2), (v_1, v_2) \in V$,其中 $u_1, v_1 \in V_1; u_2, v_2 \in V_2$。
令 $E$ 满足,$\left( \left( u_1, u_2 \right), \left( v_1, v_2 \right) \right) \in E$ 当且仅当 $\left( u_1, v_1 \right) \in E_1 \wedge \left( u_2, v_2 \right) \in E_2$。则 $G$ 和 $H$ 的张量积定义为 $G \times H = \left( V, E \right)$。
例子:下图中,左边和上面两张图的张量积是右边那张图。

字典积 (Lexicographic product):
强积 (Strong product):对无向简单图 $G = \left( V_1, E_1 \right), H = \left( V_2, E_2 \right)$,它们的强积定义为它们笛卡尔积和张量积的并,记作 $G \boxtimes H = \left( G \boxdot H \right) \cup \left( G \times H \right)$。
例子:下图中,左边和上面两张图的强积是右边那张图。
对于无向简单图,我们还能定义如下一元运算:
补图 (Complement graph):在 #10 中已经介绍。
删除一条边:对图 $G = \left( V, E \right)$,删去边 $e$ 后的图简记作 $G \setminus \{e\}$。:
缩边 (Edge contraction):
线图 (Line graph):
对于无向简单图,我们还能定义如下二元关系:
……
对于无向图 $G = \left( V, E \right)$,若 $S \subseteq V$ 满足 $G \left[ S \right]$ 是连通图,且不存在一个 $S$ 的真超集 $T$ 满足此性质 (即 $G \left[ T \right]$ 是连通图),则称 $S$ 是 $G$ 的一个连通分量 (Connected component),也称为连通块。
$G$ 的所有连通分量构成了点集 $V$ 的一个划分 (即两两交集为空,所有集合并集为 $V$)。
对于无向简单图 $G = \left( V, E \right)$,$u, v \in V$ 满足 $u \neq v$ 且 $\left( u, v \right) \notin E$。若存在点集 $S \subseteq V \setminus \left\{ u, v \right\}$ 使得在 $G \left[ V \setminus S \right]$ 中 $u, v$ 不连通,则称 $S$ 的 $u, v$ 的局部点割集 (Local vertex separating set)。如果点集 $S$ 是某个点对 $\left( u, v \right)$ 的局部点割集,则称 $S$ 是 $G$ 的全局点割集 (Global vertex separating set)。在不引起混淆的情况下,它们都可以简称点割集。
对于两个不相邻的顶点 $u, v$,定义 $u, v$ 的局部点连通度 (Local vertex connectivity) 为 $u, v$ 的局部点割集大小的最小值,记为 $\kappa \left( u, v \right)$,在不引起混淆的情况下可简称点连通度。
定义 $G$ 的全局点连通度 (Global vertex connectivity) 所有全局点割集大小的最小值,记为 $\kappa \left( G \right)$,在不引起混淆的情况下可简称点连通度。如果不存在这样的点割集,可以证明此时 $G$ 为完全图 $K_n$,定义 $\kappa \left( K_n \right) = n$。
同样,对于无向图 $G = \left( V, E \right)$ (允许有重边,但一般默认没有自环) 和 $u, v \in V$ ($u \neq v$),如果存在边集 $F \subseteq E$ 使得在 $G \setminus F$ 中 $u, v$ 不连通,则称 $F$ 是 $u, v$ 的局部边割集 (Local edge separating set)。如果边集 $F$ 是某个点对的 $\left( u, v \right)$ 的局部边割集,则称 $F$ 是 $G$ 的全局边割集 (Global edge separating set),在不引起混淆的情况下,它们都可以简称边割集。
定义 $u, v$ 的局部边连通度 (Local vertex connectivity) 为 $u, v$ 的局部边割集大小的最小值,记为 $\lambda \left( u, v \right)$,在不引起混淆的情况下可简称边连通度。
定义 $G$ 的全局边连通度 (Global vertex connectivity) 所有全局边割集大小的最小值,记为 $\lambda \left( G \right)$,在不引起混淆的情况下可简称边连通度。如果不存在这样的边割集,当且仅当 $\left| G \right| = 1$ ($G$ 只有一个顶点)。此时定义 $\lambda \left( K_1 \right) = + \infty$。(而对 $n \geq 2$ 有 $\lambda \left( K_n \right) = n - 1$)。
对于 $k \in \mathbb N$,若 $\kappa \left( G \right) \geq k$,则称 $G$ 是 $k-$点连通图 ($k-$vertex-connected graph) (也可以称 $G$ 是 $k-$点连通的),$G$ 的这一性质称作 $k-$点连通性 ($k-$vertex-connectivity)。
对于 $k \in \mathbb N$,若 $\lambda \left( G \right) \geq k$,则称 $G$ 是 $k-$边连通图 ($k-$edge-connected graph) (也可以称 $G$ 是 $k-$边连通的),$G$ 的这一性质称作 $k-$边连通性 ($k-$edge-connectivity)。
Warning 3:在大多数文献中,若没有明确指出是点连通还是边连通 (如直接使用 $k-$connected graph),则一般认为其是指点连通。
所有图 $G$ 都是 $0-$点连通且 $0-$边连通的,$G$ 是连通图当且仅当 $G$ 是 $1-$点连通图,当且仅当 $G$ 是 $1-$边连通图。
对于非完全图的无向简单图 $G$,有 $$ \kappa \left( G \right) \leq \lambda \left( G \right) \leq \delta \left( G \right) \tag 3 \label 3 $$
对于无向简单图 $G$,若单点集 $\left\{ v \right\}$ 为 $G$ 的全局点割集,则称 $v$ 是 $G$ 的割点 (Cut vertex)。可以发现,一个点是割点当且仅当 $G \setminus \left\{ v \right\}$ 的连通分量个数大于 $G$ 的连通分量个数。
若 $G$ 是 $2-$点连通图,也称 $G$ 是点双连通图 (Vertex-biconnected graph) (也可以称 $G$ 是点双连通的),$G$ 的这一性质也可称作点双连通性 (Vertex-biconnectivity)。
$G$ 是 $2-$点连通图,当且仅当 $G$ 没有割点。
同样,对于无向图,若单边集 $\left\{ e \right\}$ 为 $G$ 的全局边割集,则称 $e$ 是 $G$ 的桥边 (Bridge),也称为割边 (注意不要和 Cut edge 混淆)。同样,一条边是桥边当且仅当 $G \setminus \left\{ e \right\}$ 的连通分量个数大于 $G$ 的连通分量个数。
若 $G$ 是 $2-$边连通图,也称 $G$ 是边双连通图 (Edge-biconnected graph) (也可以称 $G$ 是边双连通的),$G$ 的这一性质也可称作边双连通性 (Edge-biconnectivity)。
$G$ 是 $2-$边连通图,当且仅当 $G$ 没有桥边。
(Menger, MFMC) 对于无向简单图 $G$,$\kappa \left( u, v \right) \geq k$ 当且仅当存在 $k$ 条从 $u$ 到 $v$ 的路径,两两之间的公共点只有 $\left\{ u, v \right\}$。
对非完全图的无向简单图 $G$,$\kappa \left( G \right) \geq k$,当且仅当对任意两点都满足上述性质。
对于无向图 $G$,$\lambda \left( u, v \right) \geq k$ 当且仅当存在 $k$ 条从 $u$ 到 $v$ 的路径,两两之间没有公共边,$\kappa \left( G \right) \geq k$ 当且仅当对任意两点都满足上述性质。
对于无向简单图 $G = \left( V, E \right)$,若 $S \subseteq V$ 满足 $G \left[ S \right]$ 是 $2-$点连通图,则不存在一个 $S$ 的真超集满足此性质,则称 $S$ 是 $G$ 的一个点双连通分量 (Vertex-biconnected component)。
不同的点双连通分量可能有公共点,公共点一定是割点。
若 $G$ 中没有孤立点,则所有点双连通分量的大小都 $\geq 2$。
$\kappa \left( u, v \right) \geq 2$,当且仅当 $u, v$ 在 $G$ 的同一个点双连通分量中。
对于 (连通的) 无向简单图 $G$,我们可以按照如下方式定义另一个无向简单图 $H = \left( B \cup C, J \right)$ (具体构造算法和本便笺无关,略):
$B$ 是 $G$ 中所有点双连通分量构成的集合。
$C$ 是 $G$ 中所有割点构成的集合。
$J$ 是这样的边 $\left( b, c \right)$ 构成的集合:其中 $b \in B, c \in b \cap C$。
则称 $H$ 是 $G$ 的块割树 (Block-cut tree)。
我们还能定义无向简单图 $H' = \left( B \cup V, J' \right)$,满足:
$J'$ 是这样的边 $\left( b, v \right)$ 构成的集合:其中 $b \in B, v \in b$。
则称 $H'$ 是 $G$ 的广义块割树 (Generalized block-cut tree) 或点双缩点树,在国内也常称为圆方树,且称集合 $B$ 中的点为 "方点",集合 $V$ 中的点为 "圆点"。
当然,可以证明,若 $G$ 是连通图,则 $G$ 的块割树和点双缩点树均为树,否则均为森林。
对于无向图 $G = \left( V, E \right)$,定义关系 $R_k : R_k \left( u, v \right)$ 当且仅当 $\lambda \left( u, v \right) \geq k$,则可以证明,$R_k$ 是 $V$ 上的等价关系。
于是 $R_k$ 将 $V$ 划分为若干个等价类 $V_1, V_2, \cdots, V_m$。称其中每个等价类为 $G$ 的一个 $k-$边连通分量 ($k-$edge-connected component)。
$2-$边连通分量又被称作边双连通分量 (Edge-biconnected component)。
Warning 4:如果对点连通定义上述概念,则 $R_k$ 不是等价关系。从 $R_2$ 中割点的存在性便可看出。
对于无向图 $G$,$S$ 是 $G$ 的边双连通分量当且仅当 $G \left[ S \right]$ 是极大的边双连通图 (即 $G \left[ S \right]$ 是边双连通图且不存在 $S$ 的真超集满足此性质)。
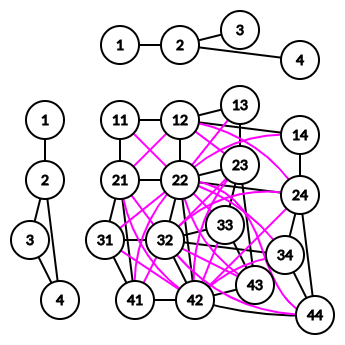
Warning 5:上述性质对 $k \geq 3$ 不成立。如下图 (当 $k \geq 3$ 时,$\left\{ 1, 2 \right\}$ 为 $G$ 的 $k-$边连通分量):
对于 (连通的) 无向图 $G$,我们可以按照如下方式定义另一个无向简单图 $H = \left( B, J \right)$:
$B$ 是 $G$ 中所有边双连通分量构成的集合。
$J$ 是这样的边 $\left( b_1, b_2 \right)$ 构成的集合:其中 $b_1, b_2 \in B$,且存在 $u \in b_1, v \in b_2$ 使得 $\left( u, v \right) \in E$。
则称 $H$ 是 $G$ 的边双缩点树。
同样,若 $G$ 连通图,则 $G$ 的边双缩点树一定是树,否则至少是森林。
注意到 $H$ 的每一条边 $\left( b_1, b_2 \right)$ 可以对应到一条边 $G$ 中的一条边 $\left( u, v \right)$。可以证明,这样对应的边是唯一的,且这条边 $\left( u, v \right)$ 是 $G$ 的桥边。
因此,对于连通图 $G$,$G$ 的桥边个数等于 $G$ 的边双连通分量个数减一。
(边三相关前置知识) $3-$边连通分量又被称作边三连通分量 (Edge-triconnected component)。
对于无向图 $G = \left( V, E \right)$,若某个二元边集 $\left\{ e_1, e_2 \right\}$ 是 $G$ 的全局边割集,且 $e_1, e_2$ 都不是桥边,则称 $\left( e_1, e_2 \right)$ 是一对切边对 (Cut pair)。
若 $G$ 是 $2-$边连通图,则 $\left( e_1, e_2 \right)$ 是切边对,当且仅当 $G \setminus \left\{ e_1, e_2 \right\}$ 不连通。
若一条非桥边 $e$ 可以和某条边 $e' \neq e$ 配合形成切边对 $\left( e, e' \right)$,则称 $e$ 是切边 (Cut edge) (注意不要和割边混淆)。
对于两个 (非桥) 边 $e_1, e_2$,定义它们切边等价 (Cut edge equivalent),当且仅当在 $G$ 的所有圈中,$e_1$ 和 $e_2$ 要么同时出现,要么同时不出现。
由这里知,切边等价是等价关系,且 $e_1, e_2$ 切边等价当且仅当 $\left( e_1, e_2 \right)$ 是切边对。
于是,切边等价关系可以将 $E$ 划分为若干个等价类 $E_1, E_2, \cdots, E_\kappa$。
若 $v \in V$ 满足 $d \left( v \right) = 2$。设 $N \left( v \right) = \left\{ u, w \right\}$ ($u$ 可以等于 $w$),则令 $H$ 为 $G$ 删去点 $v$ 后加入 $\left( u, w \right)$ 的图 (自环就不加了),则:$G$ 的 $3-$边连通分量就是 $H$ 的所有 $3-$边连通分量,再额外补上 $\left\{ v \right\}$。
若 $e = \left( u, v \right)$,满足它所在的等价类的大小为 $1$ (等价地,它不是切边),则 $u$ 和 $v$ 一定在同一个 $3-$边连通分量中。令 $H$ 为 $G \cdot e$ (缩边),则 $G$ 的 $3-$边连通分量就是 $H$ 的所有 $3-$边连通分量 (注意 $u$ 和 $v$ 再最后要展开)。
根据上述两条性质,可以得到一个在 $O \left( n \cdot \alpha \left( n \right) \right)$ 时间内求图的 $3-$边连通分量的算法 (和熟知的可能不同),见 $3-$边连通分量的另一种算法。