scx 正在使用一个有趣的数据结构——金字塔。
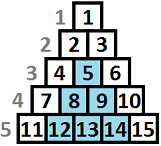
金字塔由 $n$ 行组成,其中第 $i$ 行有 $i$ 个格子组成。每一行的最左端相对于上一行左移了半个格子的宽度,金字塔上的格子由 $1$ 到 $\dbinom {n+1} 2$,从上至下,从左至右的编号。
下图是一个 $n = 5$ 的例子:

这个神奇的数据结构能接受下列两种操作:
1 i v。其中 $i$ 为格子的编号,$v$ 为改变后的值。2 i v1 v2 ... vs,其中 $i$ 为子金字塔顶的格子的编号,$s$ 为子金字塔的大小 (如上图中是 $6$),$v_i$ 为对应修改后的值。(可以不改变,即 $v_i$ 为之前的值)正式地,一个以 $i$ 行 $j$ 列为顶的子金字塔会包含行 $i \sim n$,其中第 $(i + p)$ 行包含格子 $j \sim (j + p)$ ($0 \leq p \leq n - i$)。
现在有两个金字塔,金字塔 $A$ 的 $k$ 个格子已经有非 $0$ 的数,而金字塔 $B$ 的所有格子都是 $0$。scx 需要寻找一个操作序列,使得当它施加在 $B$ 上后,能使 $B$ 中的所有格子与 $A$ 中的对应格子均相等。
在她的计算机中,执行一条指令的时钟周期数等于该操作序列的长度。因此,在众多合法操作序列中,她希望找到一条长度最短的操作序列 (时钟周期最短的),请你帮她求出操作序列的长度的最小可能值。
第一行包含两个正整数 $n, k$ ($n, k \leq 10^5$),分别表示金字塔的行数与非 $0$ 数的个数。
接下来的 $k$ 行,每行包含两个正整数,第 $i + 1$ 行的整数 $r_i, c_i$ ($1 \leq c_i \leq r_i \leq n$) 描述其中一个非 $0$ 数所在的格子的行数和列数,保证同一个格子不会被描述超过一遍。
输出一行一个整数,表示操作序列的长度的最小可能值。
由于计算机不方便支持这样的结构,所以我们将金字塔稍微倾斜一下,变成一个等腰直角三角形,如下图:
由此可以轻松地把原来的 $r_i, c_i$ 转化为现在的 $x_i, y_i$ 坐标,公式如下:
\begin{array}l x_i = n - r_i + c_i\\ y_i = n - r_i + 1 \end{array}
可以看出,一列至多使用一个塔形赋值。
考虑区间 DP,记 $f_{i, j}$ ($0 \leq j \leq i \leq n$) 表示第 $i$ 列准备使用高度为 $j$ 的子金字塔,则修改剩下的那个类似梯形的区域的最小花费,比如下图,则表示准备使用黄色部分,$f_{i, j}$ 为蓝色部分所需要的最小花费。
则可以看出,答案就应该是 $f_{n, 0}$。
记第 $i$ 列高度 ($y$ 坐标) 大于等于 $j$ 中的 $i - j + 1$ 个格子中,有 $s_{i, j}$ 个非 $0$ 格,则转移方程如下:
$$ f_{i, 0} = \min \left\{ f_{i-1, 0} + 3s_{i, 1}, \min_{1 \leq k \leq i} \left\{ f_{i-1, k-1} + \left( \frac 12 k^2 + \frac 12 k + 2 \right) + 3s_{i, k+1} \right\} \right\} $$
对于一般的 $f_{i, j}$ ($j \geq 1$),转移方程为
$$ f_{i, j} = \min \left\{ f_{i, j-1}, f_{i-1, j-1} + 3s_{i, j+1} \right\} $$
这样就得到了一个时间复杂度为 $O(n^2)$ 的做法,显然过不去,因此继续考虑优化。
可以发现,选择太大的子金字塔其实是没有意义的。
由于单点赋值只需花费 $3$,因此 $k$ 个点均单点赋值至多花费 $3k$,所以答案不会超过 $3k$。
由于高度为 $h$ 的塔形赋值需要花费 $\dfrac 12 h^2 + \dfrac 12 h + 2$,因此可以得到 (比较松) $h < \sqrt{6k}$。
因此第二维的 $j$ 只需要枚举到 $h_{\max} = \sqrt{6k}$,那么总时间复杂度为 $O(n \sqrt k)$。
而这样 DP,空间也是 $O(n \sqrt k)$,可能比较紧,然而这可以通过滚动数组或者像背包一样缩掉一维来解决,空间复杂度 $O(n + k)$。
#include <bits/stdc++.h>
#define N 100034
#define H 800
using namespace std;
typedef pair <int, int> pr;
int n, h, r, c;
int i, j, k, x, y;
int f[2][N], s[N], *F = f[0], *G = f[1];
pr V[N];
inline void down(int &x, const int y) {x > y ? x = y : 0;}
int main(){
scanf("%d%d", &n, &k);
h = min(n, (int)sqrt(6 * k));
for(i = 0; i < k; ++i){
scanf("%d%d", &r, &c);
x = n - r + c; y = n - r + 1;
V[i] = pr(x, y);
}
sort(V, V + k);
memset(f, 127, sizeof f);
F[0] = x = 0;
for(i = 1; i <= n; ++i){
y = min(i, h);
memset(G, 127, y + 2 << 2);
memset(s, 0, y + 2 << 2);
for(; x < k && V[x].first == i; ++x) ++s[V[x].second > y ? y + 1 : V[x].second];
for(j = y; j >= 0; --j) s[j] += s[j + 1];
G[0] = F[0] + s[1] * 3;
for(j = 1; j <= y; ++j)
down(G[0], F[j - 1] + (j * (j + 1) >> 1) + 2 + s[j + 1] * 3);
for(j = 1; j <= y; ++j){
G[j] = G[j - 1];
down(G[j], F[j - 1] + s[j + 1] * 3);
}
swap(F, G);
}
printf("%d\n", F[0]);
return 0;
}
坑1:在计算 s[] 数组的时候,由于空间限制 ($O(n \sqrt{6k})$,不能开两维 (当然你愿意卡也是可以的),因此可以对每一个 $x$ 坐标开一个 vector <int>,存储对应的 $y$ 坐标。
坑2:可能是姿势有点问题,我用 vector <int> 写的居然 TLE 了,其实这个根本不需要 vector <int>,将所有点转化为 $x_i, y_i$ 坐标后按照 $x$ 坐标排序,然后线性扫描过来,遇到 $x_j = i$ 的将 $s_{i, j}$ 自增,最终求个前缀和即得 $s_{i, j}$。