众所周知,大连 24 中是一所神奇的学校,在那里,化竞的同学很多都擅长写代码。
有一天,化学不及格的胡小兔向化竞巨佬晴岚请教化学题:
“$n$ 个碳原子的烷基共有多少种同分异构体?”
刚刚得了化竞全市第一的晴岚听了,认为这道题十分简单,建议胡小兔写个程序解决这个问题。但胡小兔弱得连什么是同分异构体都不知道,于是晴岚给胡小兔画了个图——例如 $n = 4$ 时 (即丁基),有 $4$ 种同分异构体:
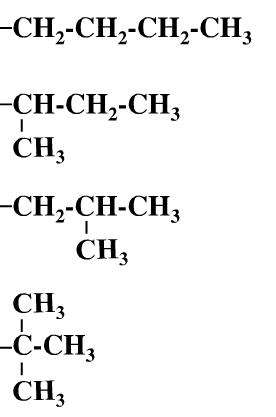
同理,其他常见烷基同分异构体数目如下表:
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
| 同分异构体数目 | $1$ | $1$ | $2$ | $4$ | $8$ | $17$ |
现在已知碳原子个数 $n$,求对应的烷基有多少种同分异构体。
注意:这里的烷基计数不用考虑空间异构,能否稳定存在等各种特殊情况。也就是说,你要求的是 $n$ 个点的每个点度数不超过 $4$ 且根的度数不超过 $3$ 的有根树的数目。
共一行,包含一个正整数 $n$ ($n \leq 5000$),表示烷基中碳原子的数目。
输出一行一个整数,表示该烷基同分异构体的数目,对 $10^9 + 7$ 取模。
第一次接触无标号树计数系列~
看起来非常恐怖,其实难度也并不是很大啦。
先来考虑有根树吧,毕竟有根的结构是更加容易 DP 的。所以我们先从烷基 (而不是烷烃) 入手来计数。
理论上,烷基计数可以做到 $O \left( n \log^2 n \right)$ 的复杂度,这里略去。
先来考虑最 simple 的 DP:用 $f_i$ 表示 $i-$烷基的个数。我们可以枚举三个子树的大小,乘上对应的二项式系数,于是得到了一个 $O \left( n^4 \right)$ 的做法。注意到 $c_1 + c_2 + c_3 = i - 1$,因此这个做法实际上是 $O \left( n^3 \right)$ 的。
但这个做法复杂度比较劣,如果碳原子能成 $100$ 个键你的复杂度就变成了 $O \left( n^{99} \right)$,显然不可接受。
那又该如何优化呢?首先,一次性枚举所有的子树显然是不靠谱的,因此可以像树形 DP 一样,一个一个子树取添加。那么具体按照什么顺序呢?对,按照子树的大小顺序添加。
我们枚举当前添加的子树大小 $size$ (从 $1$ 到 $n$),然后去对所有的 DP 值产生贡献。或者等价地,我们在 DP 最前面加一维 $s$,表示当前允许的子树大小。
我们再加一维 $j$,表示当前根节点的度数,于是我们得到了新的状态:
用 $f_{s, i, j}$ 表示在 $i-$烷基中,根节点的度数为 $j$,所有子树的大小不超过 $s$ 的方案数。
考虑转移,首先,如果所有子树的大小都小于 $s$,方案数就是 $f_{s - 1, i, j}$。否则,设有 $k$ ($1 \leq k \leq \min \left\{ j, \left \lfloor \dfrac {i-1} s \right \rfloor \right\}$) 个子树的大小为 $s$,则把这些子树去掉后,剩下的点数为 $i - s k$,根度数为 $j - k$,子树大小不超过 $s - 1$,对应到状态就是 $f_{s - 1, i - s k, j - k}$。
然后就是将大小为 $s$ 的 $k$ 个子树填充进去。设大小为 $s$ 的子树 ($s-$烷基) 有 $A_s$ 个 ($A_s = \sum f_{s-1, s, j}$)。易知,这是一个可重组合,方案数为 $\dbinom {A_s + k - 1} k$。于是就有
$$ f_{s, i, j} = \sum_{0 \leq k \leq j \\ s k < i} f_{s - 1, i - s k, j - k} \cdot \dbinom {A_s + k - 1} k $$
这样时间复杂度就是 $O \left( n^2 m \log m \right)$ 了,其中 $m$ 是碳原子的成键个数 (即树的度数限制)。
根据背包 DP 的优化方式,具体实现时,$s$ 这一维只需要枚举,不需要存储,不过需要注意 $i$ 需要从大到小枚举。于是空间复杂度为 $O \left( n m \right)$。
#include <bits/stdc++.h>
typedef long long ll;
const int N = 5100, B = 4;
const ll mod = 1000000007, inv6 = (mod + 1) / 6;
int n, size;
int f[N][B];
ll C(int n, int r) {
switch (r) {
case 0 : return 1;
case 1 : return n % mod;
case 2 : return n * (n - 1ll) / 2 % mod;
default : return n * (n - 1ll) % mod * (n - 2ll) % mod * inv6 % mod;
}
}
int main() {
int i, j, k, cur;
scanf("%d", &n);
f[1][0] = 1;
for (size = 1; size < n; ++size) {
cur = std::accumulate(f[size], f[size] + B, 0ll) % mod;
for (i = n; i; --i)
for (j = 1; j < B; ++j)
for (k = 1; k <= j && size * k < i; ++k)
f[i][j] = (f[i][j] + f[i - size * k][j - k] * C(cur + k - 1, k)) % mod;
}
printf("%lld\n", std::accumulate(f[n], f[n] + B, 0ll) % mod);
return 0;
}
坑1:这道题中由于组合数的下指标只到 $3$,因此可以分类讨论直接计算。
坑2:注意 std::accumulate 函数的使用方式,最终返回值的数据类型和传入的最后一个参数的类型一致 (long long)。