捉迷藏 Jiajia 和 Wind 是一对恩爱的夫妻,并且他们有很多孩子。某天,Jiajia、Wind 和孩子们决定在家里玩捉迷藏游戏。
他们的家很大且构造很奇特,由 $N$ 个屋子和 $N-1$ 条双向走廊组成,这 $N-1$ 条走廊的分布使得任意两个屋子都互相可达。
游戏是这样进行的:孩子们负责躲藏,Jiajia 负责找,而 Wind 负责操纵这 $N$ 个屋子的灯。在起初的时候,所有的灯都没有被打开。
每一次,孩子们只会躲藏在没有开灯的房间中,但是为了增加刺激性,孩子们会要求打开某个房间的电灯或者关闭某个房间的电灯。为了评估某一次游戏的复杂性,Jiajia 希望知道可能的最远的两个孩子的距离 (即最远的两个关灯房间的距离)。
我们将以如下形式定义每一种操作:
C(hange) i 改变第 $i$ 个房间的照明状态,若原来打开,则关闭;若原来关闭,则打开。
G(ame) 开始一次游戏,查询最远的两个关灯房间的距离。
第一行包含一个正整数 $N$ ($N \leq 10^5$),表示房间的个数,房间将被编号为 $1, 2, 3, \cdots, n$ 的整数。
接下来 $N-1$ 行每行包含两个整数 $a, b$,表示房间 $a$ 与房间 $b$ 之间有一条走廊相连。
接下来一行包含一个正整数 $Q$ ($Q \leq 5 \times 10^5$),表示操作次数。
接下来 $Q$ 行,每行一个操作,如上文所示。
对于每一个操作 Game,输出一个非负整数,表示最远的两个关灯房间的距离。若只有一个房间是关着灯的,输出 $0$;若所有房间的灯都开着,输出 $-1$。
这道题要用到括号序列的有关两点之间的路径的一个性质。
先扯括号序列的定义,一棵树的括号序列为长度为 $3n$ 的序列,每个点 $v$ 入栈时加一个 ( 和 $v$,出栈时加一个 ),如下面这棵树 (样例) 的括号序列就是 (1(2(3(4)(5)(6(7)(8)))))。
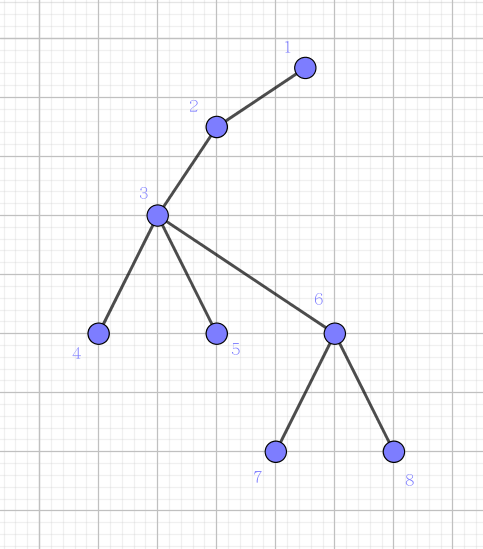
于是就有,对于任意两点 $u, v$,我们将括号序列中从 $u$ 到 $v$ 的一段 (子串) 取出来,并把数字和匹配的括号去掉,则剩余的括号数就是 $u$ 到 $v$ 的距离。比如 $4$ 和 $8$,取出的子串为 4)(5)(6(7)(8,把其中的数字和匹配的括号去掉,即得)((,剩余的括号数 $3$ 就是 $4$ 到 $8$ 的距离。
接下来要维护的就是将匹配的括号去掉后的剩余的括号数,使它们最大的一对节点。可以看出,将匹配的括号去掉后,剩下的串一定是若干个 ) 紧接着若干个 (,即 ))...)((...(。并且还有若干次修改 (切换某些点的有效和无效,其中关灯房间为有效)。
尝试使用线段树,我们要维护这么几个信息:
l (Left bracket): 该区间内 (去掉匹配括号后,下同) 剩余的 ) 数 (可以看出都在左边);
r (Right bracket): 该区间内剩余的 ( 数 (可以看出都在右边);
lc (Left bracket count): 该区间内,有效点到左端点的括号数的最大值 (例:段 ))A)))(B(C( 的 lc 值为 $7$,因为有效点 $C$ 到左端点的 (左边的) 括号数为 $7$);
rc (Right bracket count): 该区间内,有效点到右端点的括号数的最大值 (例:上面的段的 rc 值为 $6$,因为有效点 $A$ 到右端点的 (右边的) 括号数为 $6$);
ld (Left bracket difference): 该区间内,有效点到左端点的 [( 数 - ) 数] 的最大值 (例:上面的段的 ld 值为 $-2$,因为有效点 $A$ 到左端点有 $0$ 个 ( 和 $2$ 个 ));
rd (Right bracket difference): 该区间内,有效点到右端点的 [) 数 - ( 数] 的最大值 (例:上面的段的 rd 值为 $0$,因为有效点 $A$ 到右端点有 $3$ 个 ) 和 $3$ 个 ();
ans (Answer): 该区间内,两个有效点之间的括号数量的最大值 (记得是去掉匹配括号后的哦),也就是答案 (例:上面的段的 ans 值为 $5$,因为有效点 $A$ 和 $C$ 之间有 $5$ 个括号)。
(scx: 为什么要维护这些奇奇怪怪的信息呢?)
可以看出,这样在合并线段树节点的时候,带来了方便。先考虑叶节点,对于一个 (,显然它的值为 {l: 0, r: 1, lc: -∞, rc: -∞, ld: -∞, rd: -∞, ans: -∞};对于一个 ),它的值就是 {1, 0, -∞, -∞, -∞, -∞, -∞} (以下省略键);对于一个有效点,它的值应为 {0, 0, 0, 0, 0, 0, -∞};对于一个无效点,它的值就为 {0, 0, -∞, -∞, -∞, -∞, -∞}。
考虑两个线段树节点 $x, y$ 的合并:($x$ 为左子树,假设 $x, y$ 内部所有匹配括号都是去掉的,但是合起来就不一定了)
l: 第一种情况,直接为 $x.l$;第二种情况,$x$ 的右端 ( 和 $y$ 的左端的部分 ) 抵消,还有多余的 ),这种情况为 $x.l - x.r + y.l$,最后只需取 $l = \max \{x.l, x.l - x.r + y.l\}$;(不论是否 $x.r > y.l$,反正取了 $\max$)
r: 完全对称地,$r = \max \{y.r, y.r - y.l + x.r\}$;
lc: 第一种情况,直接为 $x.lc$;第二种情况,$x$ 的右端 ( 和 $y$ 的左端的部分 ) 抵消,还有多余的 ),因此为 $x.l - x.r + y.lc$;第三种情况:若 $x$ 的右端 ( 与 $y$ 的左端 ) 抵消后,$x$ 的右端 ( 还有冗余,则为 $x.l + x.r + y.ld$,故 $lc = \max \{x.l, x.l - x.r + y.lc, x.l + x.r + y.ld\}$;
rc: 完全对称地,$rc = \max \{y.r, y.r - y.l + x.rc, y.r + y.l + x.rd\}$;
ld: 这个相对简单点。第一种情况,直接为 $x.ld$;第二种情况,由于无需考虑匹配的括号 (因为它抵消了),于是按照定义就是左端的 $x.r - x.l$ 加上右端的 $y.ld$,即 $ld = \max \{x.ld, x.r - x.l + y.ld\}$;
rd: 完全对称地,$rd = \max \{y.rd, y.l - y.r + x.rd\}$;
ans: 第一种情况,两端的 $x.ans, y.ans$;第二种情况,$x$ 右端 ( 多余,为 $x.rc + y.ld$;第三种情况,$y$ 左端 ) 多余,为 $x.rd + y.lc$,故 $ans = \max \{x.ans, y.ans, x.rc + y.ld, x.rd + y.lc \}$。
最后询问的时候比较简单,直接取根节点的 ans 值即可;修改亦不难,直接单点修改,一路 update() 上去。时间复杂度为 $O(N + Q \log N)$。
#include <bits/stdc++.h>
#define N 100034
#define E 256101
#define INF 0xc0c0c0c0
using namespace std;
char op;
int n, q, e, remain;
int u, v, i;
int to[E], first[N], next[E];
int cnt = 0, id[N], val[N * 3];
inline int Max(const int x, const int y) {return x < y ? y : x;}
inline int Max(const int x, const int y, const int z) {return Max(Max(x, y), z);}
namespace ST{
#define segc int M = L + R - 1 >> 1, lc = id << 1, rc = lc | 1
struct node{
/*
l: ')', r: '(', lc, rc: '))...)((...(',
ld: '((...(' - '))...)', rd: '))...)' - '((...('
*/
int l, r, lc, rc, ld, rd, ans;
node (int v = 0): l(0), r(0), lc(INF), rc(INF), ld(INF), rd(INF), ans(INF) {
switch(v){
case -1: r = 1; break;
case -2: l = 1; break;
case 1: lc = rc = ld = rd = 0; break;
}
}
}x[N * 12];
inline node merge(const node x, const node y){
node ret = 0;
ret.l = Max(x.l, x.l - x.r + y.l);
ret.r = Max(y.r, y.r - y.l + x.r);
ret.lc = Max(x.lc, x.l - x.r + y.lc, x.l + x.r + y.ld);
ret.rc = Max(y.rc, y.r - y.l + x.rc, y.r + y.l + x.rd);
ret.ld = Max(x.ld, y.ld + x.r - x.l);
ret.rd = Max(y.rd, x.rd + y.l - y.r);
ret.ans = Max(Max(x.ans, y.ans), x.rc + y.ld, x.rd + y.lc);
return ret;
}
void build(int id, int L, int R){
if(L == R) {x[id] = node(val[L]); return;}
segc; build(lc, L, M); build(rc, M + 1, R);
x[id] = merge(x[lc], x[rc]);
}
void adj(int id, int L, int R, int h){
if(L == R) {x[id] = node(val[L]); return;}
segc; h <= M ? adj(lc, L, M, h) : adj(rc, M + 1, R, h);
x[id] = merge(x[lc], x[rc]);
}
}
inline void addedge(int u, int v){
to[++e] = v; next[e] = first[u]; first[u] = e;
to[++e] = u; next[e] = first[v]; first[v] = e;
}
void dfs(int x, int px){
int i, y;
val[++cnt] = -1;
val[++cnt] = 1; id[x] = cnt;
for(i = first[x]; i; i = next[i])
if((y = to[i]) != px)
dfs(y, x);
val[++cnt] = -2;
}
int main(){
scanf("%d", &n);
for(i = 1; i < n; ++i){
scanf("%d%d", &u, &v);
addedge(u, v);
}
remain = n; dfs(1, 0);
ST::build(1, 1, cnt);
for(scanf("%d", &q); q; --q)
if(scanf("%1s", &op), op == 67){
scanf("%d", &v);
(val[v = id[v]] ^= 1) ? ++remain : --remain;
ST::adj(1, 1, cnt, v);
}else{
if(remain <= 1) printf("%d\n", remain - 1);
else printf("%d\n", ST::x[1].ans);
}
return 0;
}
注意到当匹配的括号去掉后,剩下的串的形式一定是 ))...)((...( 的形式,就可以用线段树 (大力分类讨论) 维护了。
坑1:注意 $l$ 是左边右括号的个数,$r$ 是右边左括号的个数,不要搞反了。