对于一个带权无向图,我们可以考察它的单调上升路径。
一条路径被称为单调上升的,如果沿着它走时的权值是单调递增的。
注意,路径由多条首尾相连的边组成,且可经过同一顶点多次。路径的长度为它包含的边数。
举例来说:下图中 $v_2 \to v_3 \to v_1 \to v_2$ 是一条单调上升路径,因为每条边的权值为 $1, 2, 4$。这条路径的长度为 $3$。更进一步的,你可以验证下图中所有的单调上升路径的长度都不超过 $3$。
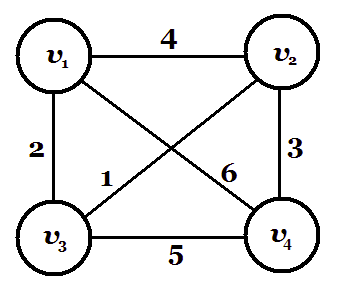
下面的结论指出在某些图中总会存在一个比较长的单调上升路径:
结论:假设带权无向图 $G$ 有 $100$ 个节点 $1000$ 条边,且所有权值各不相同。那么,$G$ 中一定存在一个单调上升路径,它的长度大于等于 $20$。
证明:假设每个节点上有一个探险家。我们按权值从小到大枚举所有的边,每次将该边连接的节点中的探险家的位置进行对调。可以知道,每个探险家都走的是一条单调上升路径。另外,由于共有 $100$ 个探险家,而探险家一共走了 $2000$ 步,所以有人走了 $20$ 步。证毕。
现在,我们的问题是:
给定一个完全图 $G$,它的顶点个数为一个偶数 $N$。
你的任务是给每条边选一个不同的权值,要使得最长的单调上升路径最短。
输入仅一行,包含一个正偶数 $N$ ($2 \leq N \leq 500$)。
输出整数 $1$ 到 $\dfrac {N(N-1)} 2$ 的一个排列,相邻的数之间用一个空格或换行隔开。
第一个数代表你给边 $(1, 2)$ 选的权值;第二个数是给 $(1, 3)$ 的权值,……,第 $N$ 个数是给 $(1, N)$ 的权值;然后是 $(2, 3)$ 的权值,$(2, 4)$ 的权值,……,$(2, N)$ 的权值;然后是 $(3, 4)$ 到 $(3, N)$ 的权值;以此类推;最后是 $(N - 1, N)$ 的权值。
我感觉这更像是一道数学的组合极值题……
我们分证明和构造两部分完成。
下面证明这个结论:若带权无向图 $G$ 有 $2n$ 个顶点和 $n (2n - 1)$ 条边,且权值互不相同。那么 $G$ 中存在一个单调上升路径,它的长度至少为 $2n - 1$。
证明:用题干给出的方法,可知探险家们一共走了 $2n (2n - 1)$ 步,所以一定有人走了 $2n - 1$ 步,证毕。
接下来就是构造啦。
在构造之前,先来讲一个概念:
对于一张图 $G$,如果它的一个生成子图 $H$ 是 $k-$正则的 (即 $\forall v \in V(H), d_H (v) = k$),则 $H$ 称为 $G$ 的一个 $k-$因子。
特殊地,$G$ 的一个 $1-$因子就是它的一个完美匹配。
下面有这样一个结论:偶数阶完全图 $K_{2n}$ 一定存在 $1-$因子分解。
注意到 $K_{2n}$ 一共有 $n (2n - 1)$ 条边,而每个 $1-$因子会有 $n$ 条边,因此 $K_{2n}$ 如果能分解,则它一定可以分为 $2n - 1$ 个 $1-$因子。
由于 $1-$因子的个数为 $2n - 1$,因此我们考虑通过 $2n - 1$ 边形来构造:
具体地,我们将 $K_{2n}$ 的 $2n - 1$ 个点 $A_0, A_2, \cdots, A_{2n-2}$ 排列到一个 (正) $2n - 1$ 边形 $P$ 上,还有一个点 $O$ 放到 $P$ 的中心处。
我们规定,第 $i$ ($i = 0, 1, \cdots, 2n - 2$) 个 $1-$因子由以下这些边构成:边 $O A_i$ 与所有以 $O A_i$ 垂直的边 $A_j A_k$,那么必须有 $j + k \equiv 2 i \pmod {2n - 1}$。可以证明这样的无序 $(j, k)$ 恰好有 $n - 1$ 对,因此这个 $1-$ 因子由 $n$ 条两两不交的边构成。
这样,我们就完成了对 $K_{2n}$ 的分解,动画演示如下 ($n = 4$):
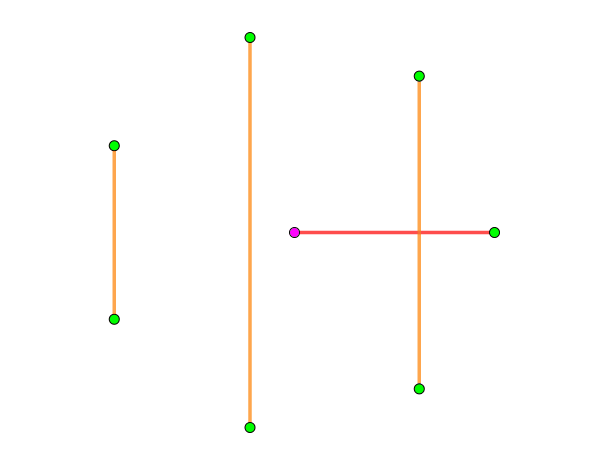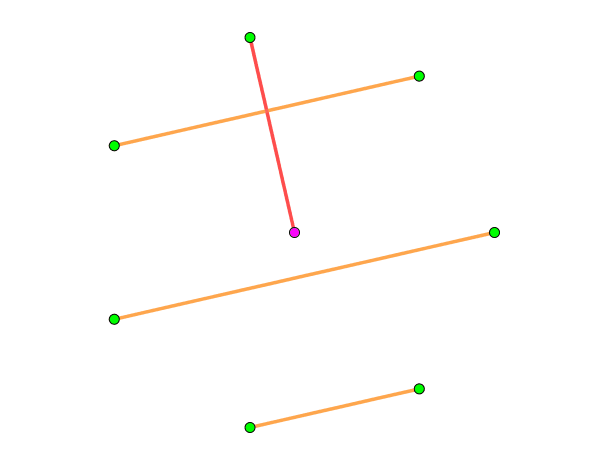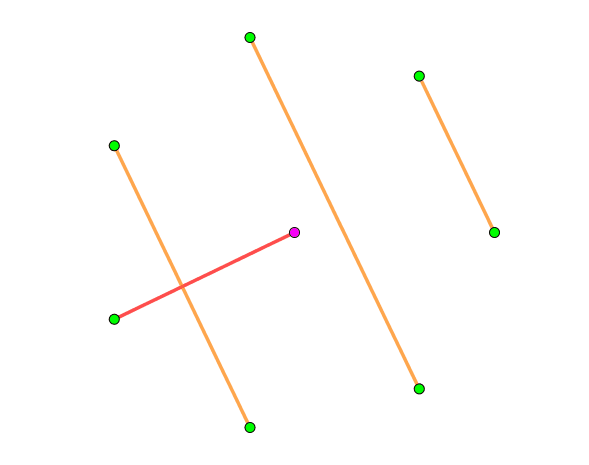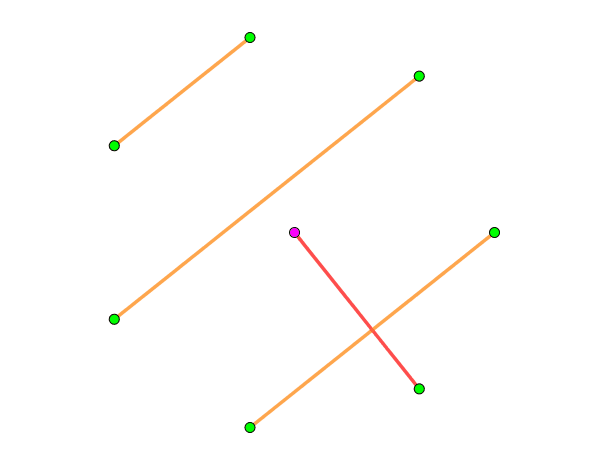
接下来的事情就简单了。我们将这个 $2n - 1$ 个 $1-$因子记作 $M_1, M_2, \cdots, M_{2n-1}$,然后对于 $\forall i < j$,令 $M_i$ 中的所有边的权值都严格小于 $M_j$ 的。这样,这张图的任何一个单调上升路径的长度都不会超过 $2n - 1$。
设 $P = \left( e_1, e_2, \cdots, e_l \right)$ 为 $G$ 的一个单调上升路径,则 $e_i.w < e_{i+1}.w$。注意到,每个 $1-$因子中不可能有相邻的两条边,因此 $e_i$ 和 $e_{i+1}$ 属于不同的 $1-$因子。而且,如果设 $e_i \in M_{y_i}$,则有 $y_i < y_{i+1}$。
这样一来,由于 $1-$因子的个数只有 $2n - 1$ 个,因此必有 $l \leq 2n - 1$,即 $P$ 的长度不超过 $2n - 1$。
最后的构造也很简单,只需让 $M_i$ 中的边权在范围 $\left( (i - 1) \cdot n, i \cdot n \right]$ 中即可。
总时间复杂度 $O \left( n^2 \right)$。
#include <bits/stdc++.h>
#define N 510
int n;
int G[N][N];
int main() {
int i, j, u, v, w = 0;
scanf("%d", &n); --n;
for (i = 0; i < n; ++i) {
G[i][n] = G[n][i] = ++w;
for (j = 1; j <= n >> 1; ++j)
u = (i - j + n) % n, v = (i + j) % n, G[u][v] = G[v][u] = ++w;
}
for (i = 0; i < n; ++i)
for (j = i + 1; j <= n; ++j)
printf("%d%c", G[i][j], j == n ? 10 : 32);
return 0;
}
坑1:在具体计算时,可以令点的编号为 $0, 1, \cdots, 2n - 2$ 和 $2n - 1$ ($O$ 点),这样在取模的时候会稍微方便一点。